Calculator Types Blog in Spanish
Blog in Spanish
El sistema RPN - una primera introducción
Las calculadoras HP41 utilizan el sistema de entrada de datos RPN (Reverse Polish Notation, o notación polaca inversa, en honor al matemático polaco Jan Lukascievic)
Este sistema difiere del algebraico normal en el orden en que se introducen los números con los que se quiere operar y el operador. Así, en una calculadora algebraica típica, para hacer una suma, el operario introduciría primero un número, después el símbolo “+”, después el otro número, y por último el signo igual, que finaliza la introduccion de datos y “obliga” a la calculadora a realizar la operación:
5 + 4 =
Y la calculadora muestra el resultado 9 en pantalla.
El sistema RPN funciona de forma diferente: primero se introduce un número, se pulsa ENTER para separarlo del segundo, se introduce el segundo y finalmente se pulsa el operador “+”:
5 ENTER 4 +
Y el resultado (no sorprendentemente) es el mismo 9.
RPN funciona con una “pila” de cuatro “cajones” o registros para los datos, llamados X, Y, Z y T. Conviene representar estos registros como una pila, estando el X abajo y el T encima. Lo que se ve en la pantalla es el registro X. Cuando el usuario pulsa la tecla ENTER, el contenido del registro X se copia en el siguiente registro (llamado “Y”). Al escribir el segundo número, éste se sobrescribe en el registro X sobre lo que había antes. Entonces tenemos:
Y - 5
X - 4
Si nos fijamos, parece como cuando hacíamos sumas y restas en la escuela: ponemos uno encima del otro. Ahora basta con pulsar la operación que se desea, y ya está.
En esta operación sencilla, el número de pulsaciones es el mismo: 4 en cada caso. No hemos ahorrado nada. Pero veamos este caso un poco mas complicado:
( 5 + 4 ) x ( 7 + 6 )
Dependiendo de si la calculadora algebraica tiene paréntesis o es una calculadora de las de andar por casa, el usuario tendrá que anotar los resultados intermedios en un papel (en el segundo caso) o escribir lo siguiente:
( 5 + 4 ) x ( 7 + 6 ) =
Total: 12 pulsaciones. Algunos sistemas de predicción de tecleo serían capaces de cerrar automáticamente el segundo paréntesis, aunque nunca el primero.
Veamos RPN. Primero contamos, y después lo repetimos a cámara lenta:
5 ENTER 4 + 6 ENTER 7 + x
Total 9 pulsaciones: un 25% menos que en el caso algebraico.
Veamos ahora cómo funciona la pila:
| LAST X | 0,000 | 0,000 | 0,000 | 4,000 | 4,000 | 4,000 | 4,000 | 7,000 | 13,000 |
| REGISTROS | |||||||||
| T | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| Z | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 9,000 | 9,000 | 0,000 | 0,000 |
| Y | 0,000 | 5,000 | 5,000 | 0,000 | 9,000 | 6,000 | 6,000 | 9,000 | 0,000 |
| X | 5,000 | 5,000 | 4,000 | 9,000 | 6,000 | 6,000 | 7,000 | 13,000 | 117,000 |
| TECLEO | 5 | ENTER | 4 | + | 6 | ENTER | 7 | + | X |
En general, los mejores resultados con RPN se obtienen trabajando desde los paréntesis más interiores a los exteriores; pero para ello hay que entender la fórmula. Para aquel que sólo quiere teclear lo que pone el libro, es más conveniente el sistema algebraico.
En RPN, el signo “-” es el operador matemático de resta. No funciona cuando lo que se quiere hacer es cambiar de signo a un número. Para ello hay que utilizar la tecla “CHS” (Change sign)
Cuando se hace alguna operación, los registros “caen” tantos pasos como se hayan utilizado. Cuando “cae” el registro T al registro Z, el contenido de T se mantiene. Es como si se fuera copiando el contenido de T indefinidamente. Esto no es un error, sino una característica deseada, que se puede utilizar con varios propósitos; por ejemplo, para utilizar una constante. Supongamos que queremos ver cómo aumenta un capital con un interés del 5% (aunque ya no existan esos intereses en depósitos…): introduciríamos 1’05 (la unidad + 5%, que es el factor de actualización); pulsaríamos ENTER tres veces, hasta que llegue al registro T; y entonces solo tenemos que introducir en X el valor del capital inicial, y pulsar indefinidamente el símbolo de multiplicación “x”.
Por último, existe otro registro llamado “Last X”. Contiene lo que había en el registro X antes de la última operación. Sirve también para varios cometidos:
- también para utilizarlo como constante, aunque en lugar de únicamente multiplicar, hay que escribir “f lastX X".
- Principalmente para deshacer errores: si se ha mutiplicado algo por un número incorrecto, se divide por lo que haya en lastX y el problema queda resuelto.
Hay veces que el resultado que uno desea no está en el lugar de la pila que uno necesita. La HP 41cl tiene varias teclas que permiten el movimiento entre niveles de la pila:
X<>y cambia los contenidos de x por y. Vale para restas y divisiones, cuando el orden de los factores no es el que queremos.
R¥ (R con la flecha hacia abajo) significa “roll down”: todos los registros rotan hacia abajo (el registro X, el de más abajo, pasa al T)
Con esta explicación inicial, el usuario puede empezar a practicar, y continuar leyendo el fantástico manual de HP, lleno de ejemplos que le ayudarán a entender esta fabulosa calculadora.
Un sistema de medición con la HP41cx
 Algunos de nosotros recordamos cuando la HP41 era lo máximo - el equivalente actual al mejor iPhone o Ipad, pero con una exclusividad mucho mayor - poca gente era capaz de dominarla. Diríamos un iPhone sólo para ingenieros.
Algunos de nosotros recordamos cuando la HP41 era lo máximo - el equivalente actual al mejor iPhone o Ipad, pero con una exclusividad mucho mayor - poca gente era capaz de dominarla. Diríamos un iPhone sólo para ingenieros.
Una de las virtudes que tenía era su capacidad de expansión. Permitía añadir módulos de memoria, reloj, puerto infrarrojo, pero también interfaces con instrumentación, como el HP-IL.
Este era un interfase increíblemente lento para los estándares actuales, funcionando a 16000 baud (comparado con los 115200 baud del RS232 y de los módems de los primero años 90, con los que nos conectábamos a internet antes de que llegara la banda ancha). Este era un sistema de bucle, en el cual los aparatos en la red estaban unidos por un cable de retorno que tenía que cerrarse para funcionar. HP principalmente fabricó estos periféricos, entre los cuales destacaba una impresora (alternativa a la impresora inicial de la HP41), pero también puentes HP-IL a HP-IB, y, sobre todo, multímetros. Entre ellos destacaba el HP 3468A/B. Este era un aparato que medía voltaje, resistencia y corriente (aunque no capacitancia). Con él se podía hacer un pequeño laboratorio y automatizar la lectura de datos (y la programación de los parámetros del multímetro) mediante pequeños programas en RPN. Yo he llegado a medir la tensión de la red a intervalos y analizarla estadísticamente, utilizado la HP41CL y el HP3468A. Y sigue sirviendo ahora, con una precisión que ya quisiera para sí el Smartstream 410 y la HP Prime.
La semana que viene pondremos a la venta un conjunto HP41CX - HP IL - HP 3468A
Mi otra pasión
 Si vienes con frecuencia a esta web, habrás visto que hay un apartado, abajo al final, de Audio. Esta es mi otra pasión. Como tal, he comprado a lo largo de mi afición un montón de equipo, pero no he sido diligente a la hora de deshacerme de él. Sin ser un coleccionista, guardaba la versión anterior de todo lo que compraba, diciéndome “tal vez lo necesite”. Pero está claro que sólo se puede escuchar un equipo de música a la vez. Por otra parte, todo ello ha sido comprado como nuevo, y cuesta deshacerse de ello a precios mucho más bajos que los originales, cuando no ha experimentado el envejecimiento y desgaste de, por ejemplo, un coche usado.
Si vienes con frecuencia a esta web, habrás visto que hay un apartado, abajo al final, de Audio. Esta es mi otra pasión. Como tal, he comprado a lo largo de mi afición un montón de equipo, pero no he sido diligente a la hora de deshacerme de él. Sin ser un coleccionista, guardaba la versión anterior de todo lo que compraba, diciéndome “tal vez lo necesite”. Pero está claro que sólo se puede escuchar un equipo de música a la vez. Por otra parte, todo ello ha sido comprado como nuevo, y cuesta deshacerse de ello a precios mucho más bajos que los originales, cuando no ha experimentado el envejecimiento y desgaste de, por ejemplo, un coche usado.
Estos días estoy poniendo en la web algo de mi equipo, usado pero en fantástico estado (casa de no fumador, sin perros ni gatos, siempre utilizándolo con volúmenes razonables). En concreto, he añadido lo siguiente:
- Un par de altavoces Anthony Gallo Nucleus Solos
- Un par de altavoces Anthony Gallo Strada
- Un amplificador Musical Fidelity KW500
- Un amplificador para auriculares electrostáticos Stax SRD-X.
- Un DAC portátil USB Audioquest Dragonfly
En el futuro cercano voy a añadir otros aparatos:
- Un lector SACD/DVD Philips 963.
- Un lector de alta gama SACD/DVD Sony DVP 9000, modificado extensamente por Vacuumstate (Level 6)
- Un pr de auriculares AK701 con caja original
En inglés hay una expresión para esto: “my loss, your gain”.
En próximos blogs hablaré sobre alguno de estos aparatos.
¿Si buscamos Pi por el exterior?
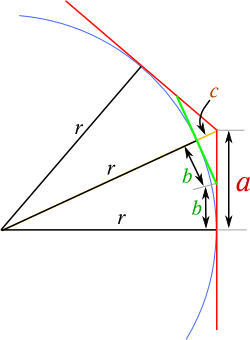 El reto de esta semana será hacer el mismo problema de la semana anterior - pero esta vez por el exterior del círculo. No es tan fácil como inicialmente se piensa; y a mí me parece claramente más sencilla la otra aproximación. Primero plantearemos las ecuaciones después de ver el dibujo adjunto. De ahí, tenéis que sacar la fórmula iterativa, y programarla en la calculadora HP de vuestra elección.
El reto de esta semana será hacer el mismo problema de la semana anterior - pero esta vez por el exterior del círculo. No es tan fácil como inicialmente se piensa; y a mí me parece claramente más sencilla la otra aproximación. Primero plantearemos las ecuaciones después de ver el dibujo adjunto. De ahí, tenéis que sacar la fórmula iterativa, y programarla en la calculadora HP de vuestra elección.
(2a) ![]()
(2b) ![]()
¡Hala! ¡A probar!
...y otra solución para la HP Prime
Me he dado cuenta que mi práctica de programación está totalmente oxidada para cualquier cosa que no sea RPN. Me cuesta un montón hacer un programa que no sea en RPN o en el BASIC original de HP. La HP Prime tiene una multitud de tipos de bucle, y me he perdido buscando el bucle que mejor se adaptara al problema que nos ocupa: cómo calcular Pi mediante el teorema de Pitágoras. Tampoco fui capaz de encontrar los medios de para r y rearrancar el programa, sin hacer chapuzas como utilizar un form de entrada y no utilizar lo entrado. Pero bueno: el programa hace lo que se quería hacer, mostrando los valores que se van consiguiendo en cada iteración.
El programa toma como entrada el diámetro, y da la circunferencia para ese radio. Lógicamente, la mejor manera de probarlo es poniendo un diámetro de 1 - con lo cual el resultado ha de ser Pi:
EXPORT Pitagoras(D)
BEGIN
LOCAL LADO, POLY, C, R;
R:=D/2;
LADO:=R*sqrt(2);
POLY:=4;
C:=LADO*POLY;
FOR I FROM 2 TO 25 DO
PRINT(C);
WAIT(2);
POLY:=POLY*2;
LADO:=sqrt((LADO/2)^2+(R-sqrt(R2-(LADO/2)2))^2);
C:=LADO*POLY;
END;
PRINT(C);
END;
Pi por teorema de Pitágoras: una posible solución para HP41c
 La semana pasada os propusimos un problema: cómo calcular Pi con vuestra calculadora, utilizando el teorema de Pitágoras. La propuesta inicial era preparar un programa para la HP Prime (que sigue en pie). Dimos como alternativa la posibilidad de crearlo para cualquier otra calculadora HP. ¿Cuál mejor que la HP41c? Como hace tiempo que no utilizo funciones de módulos, decidí usar sólo funciones standard, no las contenidas en módulos como el SOLVE del Advantage pack.
La semana pasada os propusimos un problema: cómo calcular Pi con vuestra calculadora, utilizando el teorema de Pitágoras. La propuesta inicial era preparar un programa para la HP Prime (que sigue en pie). Dimos como alternativa la posibilidad de crearlo para cualquier otra calculadora HP. ¿Cuál mejor que la HP41c? Como hace tiempo que no utilizo funciones de módulos, decidí usar sólo funciones standard, no las contenidas en módulos como el SOLVE del Advantage pack.
Como dijimos, hemos utilizado el polígono circunscrito en la circunferencia, doblando el número de lados del polígono en cada iteración. Este método se tiende a pi "por debajo". Una solución alternativa, que utilizaremos otro día se basa en el polígono cuyos lados son tangentes al círculo, y tiende a Pi "por encima".
El programa encuentra promero el lado del cuadrado inscrito en la circunferencia mediante el teorema de Pitágoras: dado r = ½ del diámetro (d), entonces el lado es l12 = r2+r2 = 2r2 => l1 = r*sqrt(2),
Desde aquí, viendo el dibujo, el siguiente polígono se puede calcular como la hipotenusa de un triángulo cuyo lado es la mitad del lado del cuadrado, y el otro lado, la diferencia entre el radio y el lado de otro triángulo, éste último con un lado que es el medio lado del polígono anterior, y como hipotenusa, el radio del círculo. Viéndolo escrito en notación matemática, es más fácil que escribiéndolo:
l(i+1) =sqrt((li/2)^2+(r-sqrt(r2-(li/2)2))^2)
Fijémonos que (li/2)^2 aparece dos veces: la única "astucia" que se me ocurre es intentar calcularlo una sóla vez cada iteración, utilizando el stack para guardar una copia para después. La belleza del RPN. Bueno, y ahorrar una tecla debido a que el cuadrado de (li/2)^2-r2 (que se puede calcular sin cambiar x por y) es igual a lo que buscamos, el cuadrado de r2-(li/2)2.
El programa para el HP41c está aquí al lado. Atención a la bella impresión, cortesía del programa i41cx+ de mi iPad. He puesto un stop (R/S) al principio del bucle, para poder ver el estado de cada iteración:
¿Alguien se atreve con el polígono exterior?
Pi mediante teorema de Pitágoras
He leído recientemente la novela “El asesinato de Pitágoras, de Marcos Chico. Es un thriller situado en el tiempo de Pitágoras, en la que se trata de algunos de los temas matemáticos de la época.
Entonces los griegos todavía no conocían Pi. Sabía knock la relación entre el diámetro y la circunferencia era algo superior a tres, pero separaban ahí. No sabían como calcularlo, aparte de medirlo, y menos se imaginaban que era un número irracional. Los pitagóricos creían que toda magnitud conocida se podía expresar como razón entre dos número enteros.
En la historia, hay un rico siracusano que ofrece una fortuna en oro a quién sea capaz de decirle la relación entre le diámetro y el radio con cuatro decimales. El villano de la novela gana con un método basado, para más INRI de los pitagoreanos, en el famoso teorema. En principio, ese era el único método de que podían disponer en aquella época para calcular Pi - el resto de los métodos actuales eran irrealizables.
La descripción de la novela no me fue suficiente. Siendo una persona visual, tuve que dibujarlo y verlo. Entonces me dispuse a calcularlo con un programa de la HP Prime, para poder más tarde enseñarlo a mi hijo. Lo comencé con este gráfico, y lo comprobé con una hoja de cálculo. Con 26 iteraciones, es igual a 15 decimales de Pi de Excel.
¿Seréis capaces de hacer un programa para la Prime que lo resuelva por este método? Si no estáis a gusto con la Prime, se permite cualquier otra calculadora HP, ya sea en RPN o RPL.
Este viernes, la solución. ¡Tenéis tres días!
Atajos en la HP Prime
Algunos atajos para la HP Prime
El “user keyboard” en la HP Prime nos permite grans flexibilidad en la configuración de nuestra calculadora. Los que habíamos usado la HP50g y la HP41c estábamos acostumbrados a esta posibilidad. No recuerdo ahora si la HP42s permitía también la configuración del teclado entero, o por el contrario sólo las teclas de función. Esto último, aunque útil, es algo totalmente diferente y que muchas HP han tenido.
A no ser que seas un estudiante con muchos campos nuevos que cubrir, cambiando cada día según las lecciones, habrá algunas funciones que utilices con mucha frecuencia y que posiblemente quieras automatizar. Yo tengo mi HP41CL completamente configurada a mi gusto - por algo es la calculadora a la que vuelvo siempre que quiero hacer algo rápido. Mientras otras me son útiles, esta es la que tiene todo lo que quiero en la punta de los dedos. Y ahora quiero hacer alga parecido con la HP PRime
El procedimiento de asignación de teclas está explicado en la página 516 del manual de usuario. Este manual no viene “impreso” con la calculadora, sino en el disco adjunto. Si no sabes dónde está, no te preocupes: lo puedes sacar del menú de ayuda en el emulador para Windows de la HP Prime. De él se desprende que sólo se puede utilizar para que devuelva un texto con la presión de la tecla deseada. Si se hace cualquier otra cosa (por ejemplo, devolver una función, nos devuelve Error 4 Syntax error, al chequear el programa.
Hay que escribir programas cortos para cada una de las teclas que hay que asignar. No te preocupes: es facilísimo, y hay “templates” (patrones) que nos ayudan a hacerlo, desde la tecla de “templates” en la pantalla de programas.
He creado un programa llamado “keys” donde guardo todas las definiciones de teclas que utilizo. Ponerlas en más sitios es una receta para tener un lío cuando se quiera cambiar la configuración. Mejor todas juntitas. Sólo con crear estos programitas y activando el teclado de usuario (ya sea para una sóla vez o en permanente) es suficiente para habilitar las teclas asignadas (Tengo que comprobar si es posible restringir el ámbito de actuación de estas asignaciones, metiendo las definiciones en los programas de las apps, para que sea sólo válido para esa app).
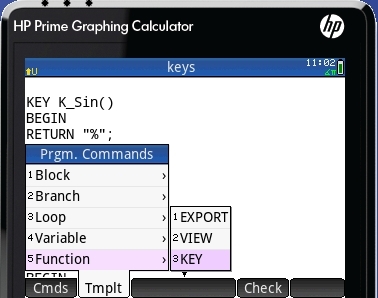 La sintaxis es muy sencilla, y, como dije antes, se puede tomar desde el menú de templates en la página de programas, como se puede ver en la foto de al lado. Utilizo un montón las funciones de porcentaje por mi trabajo, y comparativamente poco o nada las trigonométricas, por lo que he asignado las funciones %, %CHANGE() y %TOTAL() (que ya existen en la Prime) a las teclas SIN, COS y TAN respectivamente:
La sintaxis es muy sencilla, y, como dije antes, se puede tomar desde el menú de templates en la página de programas, como se puede ver en la foto de al lado. Utilizo un montón las funciones de porcentaje por mi trabajo, y comparativamente poco o nada las trigonométricas, por lo que he asignado las funciones %, %CHANGE() y %TOTAL() (que ya existen en la Prime) a las teclas SIN, COS y TAN respectivamente:
KEY K_Sin()
BEGIN
RETURN “%”;
END;
KEY K_Cos()
BEGIN
RETURN “%CHANGE()”;
END;
KEY K_Tan()
BEGIN
RETURN “%TOTAL()”;
END;
¿Qué hace esto? Simpelente la calculadora escribe lo que está entre comillas en la posición del cursor.
Atanción: podemos también retrogradar las combinaciones de teclas con shift, alpha y shift alpha, cambiando ligeramente el template:
K_ es la tecla principal
KS_ es para la tecla con shift
KA_ es para las alfanumericas
KSA_ es para las alfanumericas con shift
El código de cada tecla se puede encontrar en la página 518 del manual.
¿Y como funciona? El resto de la discusión asume que el método de entrada de datos es RPN.
Imaginemos que queremos calcular 25% de 235. Escribimos 235, enter, 25, SIN, se añade un “%” al 25, pulsamos enter, y ya tenemos el resultado. Fijémonos que no tuvimos que separar el % del número - pero tampoco chocaba a la vista.
Ahora esto otro: queremos ver el porcentaje de cambio entre 235 y 200. Pulsamos 235, enter, 200, COS, y esto es lo que se ve en la pantalla:
235
200%CHANGE()
Esto sí que es feo. Por supuesto que podemos pulsar enter después del 200, después COS, y después enter otra vez. ¡Pero ya es una tecla de más! Igual pasa si ponemos un espacio antes del COS
Aunque resulte feo, lo de arriba SI funciona.
Y como funciona así, no metería yo un espacio dentro del programa de asignación de tecla. Todavía nos puede causar un error en otro sitio.
El firmware de la HP 15c
Acaba de salir la última versión del sistema operativo para Apple Mac, Yosemite. Hay muchas nuevas características, pero también corrección de muchos pequeños errores del software anterior. Hay cosas que todavía no he conseguido hacer bien con Mavericks. Esto es típico del software actual: debido a su propia complejidad, está lleno de errores, y tiene fallos funcionamiento que en muchos casos impiden su uso en aplicaciones “mission critical”.
Comparemos eso con la ROM con 12k palabras de 10 bit que tenía la HP15c. Ese código estaba lleno de magníficas rutinas matemáticas que permitían a esa calculadora hacer operaciones con matrices, integrales, búsqueda de soluciones de ecuaciones, etc. Y muchas de las HP15c que se han fabricado, si no han sido maltratadas desde el punto de vista físico, siguen funcionando: tan resistente era el modelo.
Y no hablemos de batería. Sobre las 7 o las 8 de cada día, mi móvil me avisa de que he llegado al 20% de batería; mientras que la HP 15c original podía durar hasta 15 años con la misma batería. No se podía actualizar, como los móviles actuales; pero tampoco hacía falta: era la calculadora de bolsillo definitiva, con todo lo que un usuario científico o técnico podía necesitar, sin tener que recurrir a un gran ordenador (recordemos que es un pelín anterior al PC)
Cada vez que me fijo en el diseño y la lógica de la HP15c, me parece uno de los objetos mejor diseñados por el hombre. Es la cumbre del “menos es más”. Además de que todas las teclas tienen tres funciones escritas en su superficie, muchas de ellas tienen más: la tecla tiene diferentes significados en función de los que se esté haciendo. Diversas transformaciones de matrices complejas se hacen utilizando las teclas de combinatoria; la tecla ”+” suma números, pero también complejos y matrices, al igual que la tecla “x”; la tecla “/“, cuando se aplica a matrices, resuelve el sistema de ecuaciones; Y el modo “user” permite resignar las teclas de debajo de la pantalla a programs, además de permitir llenar secuencialmente una matriz.
Tenía 10 dígitos de precisión, que era “lo más” en aquella época para una calculadora de bolsillo. Ahora, 14 y 16 dígitos son normales; pero ¿cuándo se necesita realmente tanta precisión? Además, no es tan importante el número de dígitos mostrados, como el número de dígitos correctos. Y las calculadoras HP de aquella época tenían los mejores algoritmos posibles. LA mayoría fueron creados por William Kahan. Además, fueron desarrollados en código máquina (ahora todo se hace en “C” o incluso en otros lenguajes más elevados, siendo por tanto mucho menos compactos y rápidos para un mismo hardware) para aprovechar al máximo el procesador.
La HP15c utilizaba una versión del procesador “nut” desarrollado para la HP41c, funcionando a una frecuencia que hoy nos parece totalmente ridícula: 244 kHz (sí, kHz, no MHz o GHz), y tardaba varios minutos en realizar una inversión de una matriz de 8x8.
Los algoritmos eran tan buenos que, cuando HP decidió sacar una nueva HP15c basada en un procesador actual, decidió usar exactamente el mismo firmware, funcionando sobre una capa de emulación del procesador “nut” sobre un procesador ARM Atmel. Hubo varios problemas al adaptar el firmware al nuevo hardware (por ejemplo, la función PSE - pausa - no funciona bien, y el indicador de batería baja no funciona cuando debería, borrándose la memoria cuando se acaba la batería)
Pero aparte de eso, es tan buena como la original - sólo que funcionan 100 veces más rápido a pesar de la emulación.
Lástima que ya no quedan más stocks, ni de una ni de otra.
La HP41c
 Durante la época de estudiante, como dije, utilicé una casio programable en Basic, que era buena y barata, pero siempre quise una HP41.
Durante la época de estudiante, como dije, utilicé una casio programable en Basic, que era buena y barata, pero siempre quise una HP41.
Esta calculadora se estuvo fabricando ininterrumpidamente durante más de 10 años. No llega a la longevidad de la hp12c (que sigue fabricándose desde 1981, y que cumplió en 2011 su 30 aniversario), pero durante toda esa época (los años 80) fue la referencia indiscutida.
¿Qué la hacía ser la referencia?
- Era una de las primeras calculadoras alfanuméricas. Su display era de gran claridad, y era de segmentos, comparados con los de pídeles, que permiten una mayor variación en las letras, pero que en aquella época carecían de suficiente contraste (baste ver algunas calculadora de la gama Pioneer, como la HP17bII o la HP42s)
- Tenía una gran capacidad de memoria para aquella época, y se podía gestionar de una forma mucho más avanzada que cualquier otra de la competencia.
- Era ampliable mediante 4 puertos de expansión en su parte trasera, tanto en sus capacidades lógicas mediante módulos ROM que almacenaban programas y funciones de áreas específicas, como en sus posibilidades de hardware, con impresoras, dispositivos de cinta, interfaces infrarrojos, y, mediante la interfaz HP-IL, toda una gama de dispositivos portátiles y de laboratorio de HP: multímetros, plotters, etc.
- Casi todas las teclas de la calculadora podían ser reasignadas a nuevas funciones o programas (user keyboard), y la calculadora venía con carátulas en que se podía escribir la nueva función que cada tecla tenía. Esas carátulas se mantenían mediante orificios en la parte inferior del teclado, y un pasador con muelle en la parte superior que las mantenía fijas.
El poseedor de una HP41c era consciente de que tenía un ordenador portátil en la mano, y que con él podía hacer casi cualquier cosa. Hay libros que indican cómo se podían controlar las luces de la casa mediante la HP41c.
El primer modelo fue la HP41c propiamente dicha, con 63 registros de memoria, que podían convertirse en pasos de programa, a razón de 7 bytes por registro, según la configuración necesaria por el usuario. En los puertos de expansión se podían añadir hasta 4 módulos de memoria de 64 registros cada uno, llegando en total hasta los 319 registros.
El segundo modelo fue la HP41cv. Incluía de serie los 319 registros en la placa base, con lo cual los cuatro puertos de expansión quedaban libres para módulos ROM (para ampliar la funcionalidad de la calculadora) o módulos de interface. (Para valorar la cantidad de memoria que tenía, baste pensar que tenía 2,23 kbytes de memoria. El iPhone más pequeño tiene 8 Gb, es decir, casi 4 millones de veces más.)
El tercer modelo fue la HP41CX. Además de lo anterior, tenía memoria extendida (memoria que no se puede acceder directamente pero de la que se puede copiar y trasladar a la memoria principal, de forma similar al límite de 640 kb de MSDOS), algunas funciones adicionales, y un módulo de reloj, con el cual llegaron las alarmas, funciones de calendario y un cronómetro. Aparentemente, el módulo de reloj se creó a petición expresa de la NASA, que había elegido la HP41c como calculadora de vuelo y quería incluir programas que actuaran en función de la posición orbital de las lanzaderas, para el caso de que el ordenador principal fallara.
(Otro artículo interesante será sobre la utilización de las HP en la carrera espacial)
Se han hecho más de 250 módulos ROM de programas y funciones adicionales a través de los años. Hay ROMs para los más variados campos de la ciencia las matemáticas y las finanzas; pero sólo se podían utilizar cuatro simultáneamente.
En los últimos años, y aprovechando los avances en miniaturización, un entusiasta ha desarrollado una placa de procesador que sustituye a la placa original, y gracias a la memoria adicional de que se dispone ahora, permite almacenar TODOS los módulos ROM existentes sin necesidad de utilizar los puertos de expansión, además de funcionar hasta 50 veces más rápido. La nueva calculadora (que necesita una calculadora “donante” original) se llama HP41CL y es una auténtica maravilla. Si tuviste (o tienes) una HP41c, deberías probar la HP41cl. Capacidad infinita de programas a todos los efectos prácticos, rapidísima, y con toda la funcionalidad desarrollada a lo largo de todos estos años, incluida de serie en el sistema.
Continuará…



