Calculator Types Blog in Spanish Posts on topic: Pi
Blog in Spanish
¿Si buscamos Pi por el exterior?
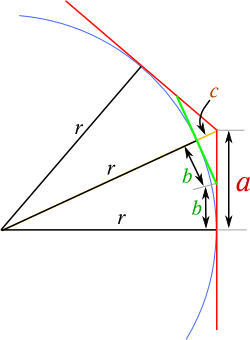 El reto de esta semana será hacer el mismo problema de la semana anterior - pero esta vez por el exterior del círculo. No es tan fácil como inicialmente se piensa; y a mí me parece claramente más sencilla la otra aproximación. Primero plantearemos las ecuaciones después de ver el dibujo adjunto. De ahí, tenéis que sacar la fórmula iterativa, y programarla en la calculadora HP de vuestra elección.
El reto de esta semana será hacer el mismo problema de la semana anterior - pero esta vez por el exterior del círculo. No es tan fácil como inicialmente se piensa; y a mí me parece claramente más sencilla la otra aproximación. Primero plantearemos las ecuaciones después de ver el dibujo adjunto. De ahí, tenéis que sacar la fórmula iterativa, y programarla en la calculadora HP de vuestra elección.
(2a) ![]()
(2b) ![]()
¡Hala! ¡A probar!
...y otra solución para la HP Prime
Me he dado cuenta que mi práctica de programación está totalmente oxidada para cualquier cosa que no sea RPN. Me cuesta un montón hacer un programa que no sea en RPN o en el BASIC original de HP. La HP Prime tiene una multitud de tipos de bucle, y me he perdido buscando el bucle que mejor se adaptara al problema que nos ocupa: cómo calcular Pi mediante el teorema de Pitágoras. Tampoco fui capaz de encontrar los medios de para r y rearrancar el programa, sin hacer chapuzas como utilizar un form de entrada y no utilizar lo entrado. Pero bueno: el programa hace lo que se quería hacer, mostrando los valores que se van consiguiendo en cada iteración.
El programa toma como entrada el diámetro, y da la circunferencia para ese radio. Lógicamente, la mejor manera de probarlo es poniendo un diámetro de 1 - con lo cual el resultado ha de ser Pi:
EXPORT Pitagoras(D)
BEGIN
LOCAL LADO, POLY, C, R;
R:=D/2;
LADO:=R*sqrt(2);
POLY:=4;
C:=LADO*POLY;
FOR I FROM 2 TO 25 DO
PRINT(C);
WAIT(2);
POLY:=POLY*2;
LADO:=sqrt((LADO/2)^2+(R-sqrt(R2-(LADO/2)2))^2);
C:=LADO*POLY;
END;
PRINT(C);
END;
Pi por teorema de Pitágoras: una posible solución para HP41c
 La semana pasada os propusimos un problema: cómo calcular Pi con vuestra calculadora, utilizando el teorema de Pitágoras. La propuesta inicial era preparar un programa para la HP Prime (que sigue en pie). Dimos como alternativa la posibilidad de crearlo para cualquier otra calculadora HP. ¿Cuál mejor que la HP41c? Como hace tiempo que no utilizo funciones de módulos, decidí usar sólo funciones standard, no las contenidas en módulos como el SOLVE del Advantage pack.
La semana pasada os propusimos un problema: cómo calcular Pi con vuestra calculadora, utilizando el teorema de Pitágoras. La propuesta inicial era preparar un programa para la HP Prime (que sigue en pie). Dimos como alternativa la posibilidad de crearlo para cualquier otra calculadora HP. ¿Cuál mejor que la HP41c? Como hace tiempo que no utilizo funciones de módulos, decidí usar sólo funciones standard, no las contenidas en módulos como el SOLVE del Advantage pack.
Como dijimos, hemos utilizado el polígono circunscrito en la circunferencia, doblando el número de lados del polígono en cada iteración. Este método se tiende a pi "por debajo". Una solución alternativa, que utilizaremos otro día se basa en el polígono cuyos lados son tangentes al círculo, y tiende a Pi "por encima".
El programa encuentra promero el lado del cuadrado inscrito en la circunferencia mediante el teorema de Pitágoras: dado r = ½ del diámetro (d), entonces el lado es l12 = r2+r2 = 2r2 => l1 = r*sqrt(2),
Desde aquí, viendo el dibujo, el siguiente polígono se puede calcular como la hipotenusa de un triángulo cuyo lado es la mitad del lado del cuadrado, y el otro lado, la diferencia entre el radio y el lado de otro triángulo, éste último con un lado que es el medio lado del polígono anterior, y como hipotenusa, el radio del círculo. Viéndolo escrito en notación matemática, es más fácil que escribiéndolo:
l(i+1) =sqrt((li/2)^2+(r-sqrt(r2-(li/2)2))^2)
Fijémonos que (li/2)^2 aparece dos veces: la única "astucia" que se me ocurre es intentar calcularlo una sóla vez cada iteración, utilizando el stack para guardar una copia para después. La belleza del RPN. Bueno, y ahorrar una tecla debido a que el cuadrado de (li/2)^2-r2 (que se puede calcular sin cambiar x por y) es igual a lo que buscamos, el cuadrado de r2-(li/2)2.
El programa para el HP41c está aquí al lado. Atención a la bella impresión, cortesía del programa i41cx+ de mi iPad. He puesto un stop (R/S) al principio del bucle, para poder ver el estado de cada iteración:
¿Alguien se atreve con el polígono exterior?
Pi mediante teorema de Pitágoras
He leído recientemente la novela “El asesinato de Pitágoras, de Marcos Chico. Es un thriller situado en el tiempo de Pitágoras, en la que se trata de algunos de los temas matemáticos de la época.
Entonces los griegos todavía no conocían Pi. Sabía knock la relación entre el diámetro y la circunferencia era algo superior a tres, pero separaban ahí. No sabían como calcularlo, aparte de medirlo, y menos se imaginaban que era un número irracional. Los pitagóricos creían que toda magnitud conocida se podía expresar como razón entre dos número enteros.
En la historia, hay un rico siracusano que ofrece una fortuna en oro a quién sea capaz de decirle la relación entre le diámetro y el radio con cuatro decimales. El villano de la novela gana con un método basado, para más INRI de los pitagoreanos, en el famoso teorema. En principio, ese era el único método de que podían disponer en aquella época para calcular Pi - el resto de los métodos actuales eran irrealizables.
La descripción de la novela no me fue suficiente. Siendo una persona visual, tuve que dibujarlo y verlo. Entonces me dispuse a calcularlo con un programa de la HP Prime, para poder más tarde enseñarlo a mi hijo. Lo comencé con este gráfico, y lo comprobé con una hoja de cálculo. Con 26 iteraciones, es igual a 15 decimales de Pi de Excel.
¿Seréis capaces de hacer un programa para la Prime que lo resuelva por este método? Si no estáis a gusto con la Prime, se permite cualquier otra calculadora HP, ya sea en RPN o RPL.
Este viernes, la solución. ¡Tenéis tres días!



