Programas financieros

As I have mentioned before, most of my duties involve financial calculations in an industrial environment. 

The calculator I prefer among all, because of its simplicity (no menus) and its portability (fits in my jacket and occupies very limited space in a crowded desk), is the HP15.

Here is a dump of the program memory:

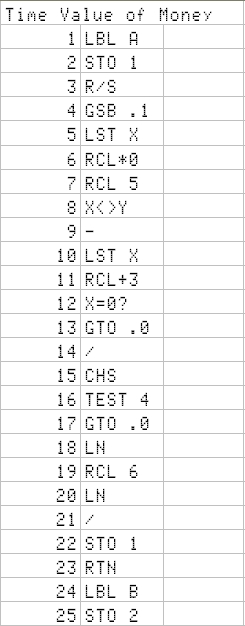
Let's start with an oldie, in the version that appears in the Advanced Functions handbook - no change needed. It uses the A to E keys in User mode, following the standard n -i- PV- PMT-FV. One key for entering the data and placing the program pointer in the right place; then R/S to execute:

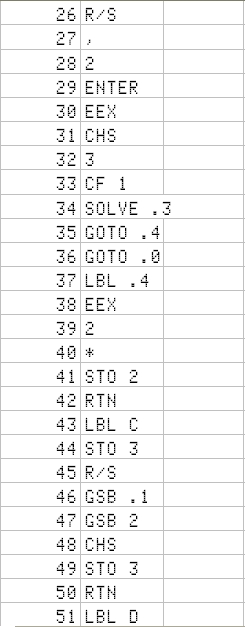
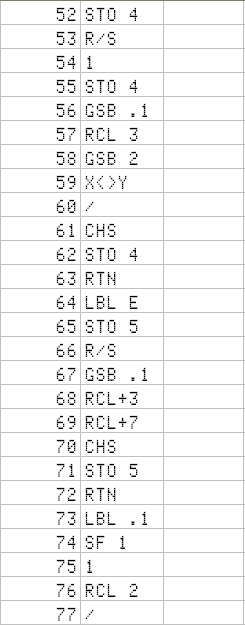
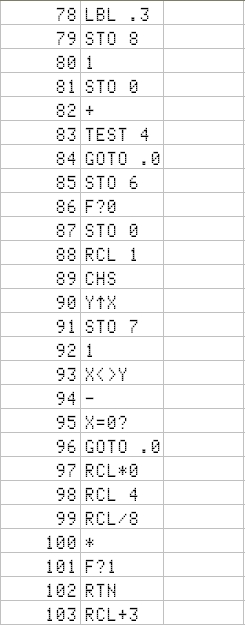
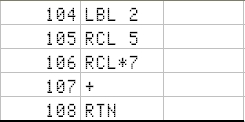
I will continue in the next few blogs with the rest of the memory. For the sake of engineer futility, I have left space enough for a 3x3 + 3 equation system if some time was needed - and it has not been the case so far !!

The NPV and IRR are other favourites. There is another program in the Advanced Functions Handbook, that allows for up to 24 groups of cashflows (assuming you do not have any other program in memory!) and using 68 steps. However, as I said before, in my company we limit Capital Expenditure Proposal analysis to 10 years, so that I set to make a shorter program for 10 cashflows. 

Register 0 is for the initial investment. Register ,1 contains the number of years to calculate (good to limit the loop and increase speed). Registers 1 to ,0 contain the flows of each year.

The system takes X as discount rate (in %). It can be then used to find the IRR through the Solve feature, entering a bracket of guesses in X and Y.

Now we come to a weighted average calculator. In many occasions I need to get the average margin of all the brands we sell.

But the weighting in HP12c works inverse as I would do. It calculates the average of Y weighted by X, instead of the average of x weighted by Y.

The calculators is mine and I do as I want with it ;-), so I will put it here, together with a cash discount calculation/comparison. We assign the weighted average to the same key, i.e. GSB 0:

One of the typical decisions in my job is to decide on cash discounts - both when buying and selling. I want to compare the cash discount % with a yearly rate - and then decide. I put the standard payment days in Y, and the discount % in X, and get the equivalent yearly interest that I am getting (if I'm buying) or I'm paying (if I'm selling)

Here it is:

As I have mentioned before, most of my duties involve financial calculations in an industrial environment. 

The calculator I prefer among all, because of its simplicity (no menus) and its portability (fits in my jacket and occupies very limited space in a crowded desk, is the HP15.

Here is a dump of the program memory:

Let's start with an oldie, in the version that appears in the Advanced Functions handbook - no change needed. It uses the A to E keys in User mode, following the standard n -i- PV- PMT-FV. One key for entering the data and placing the program pointer in the right place; then R/S to execute:

For the sake of engineer futility, I have left space enough for a 3x3 + 3 equation system if some time was needed - and it has not been the case so far !!

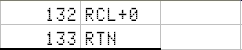
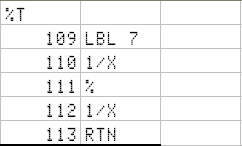
Here you have a small function missing in the 15c: the %T !!

I have placed it close to its siblings: in the GSB 7 key:

I loved its simplicity since I saw it in an HP41cv manual:

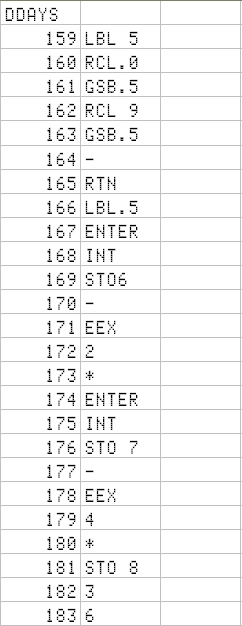
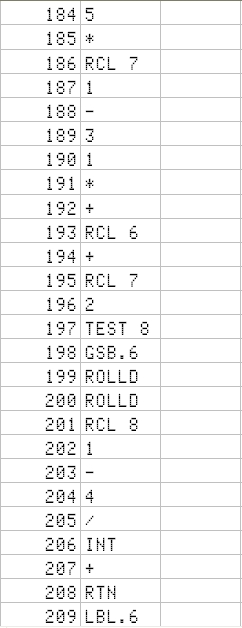
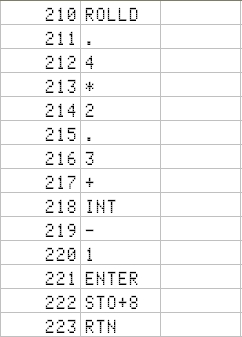
Finally, I include date calculations. The one I use more is the HP12c's DDAYS operation. I then set to find in the web software for it. I did not find it for the 15c, but I did for the 42s, that I then adapted. Attention - it has been modified to cater for European date format: dd.mmyyyy - you will have to go to the part where it decomposes the number into the parts and then change a few lines there.

The strategy is just to convert the date format to Julian number, convert the other date, and subtract. Fortunately, the DtoJ subroutine does not consume all 4 stack registers - or we would not be able to subtract them!

Once entered, you will still have 16 registers left. (we assume that we have set 11 registers for program use: from register 0 to .1 (so that you can enter the investment + 10 years + the number of years for the IRR program seen in past article). These 16 free registers allow you to invert a 4x4 matrix, or to solve 2 equation systems with the same coefficient matrix (a typical thing when you're solving structure problems - you apply the same set of linear equations to different conditions)

Here it is (and I have finished with it. The only possible addition would be the DATE+ function. The D->J is a part of the DDAYS program; We would just need to create the J->D - at the expense of losing necessary registers!)